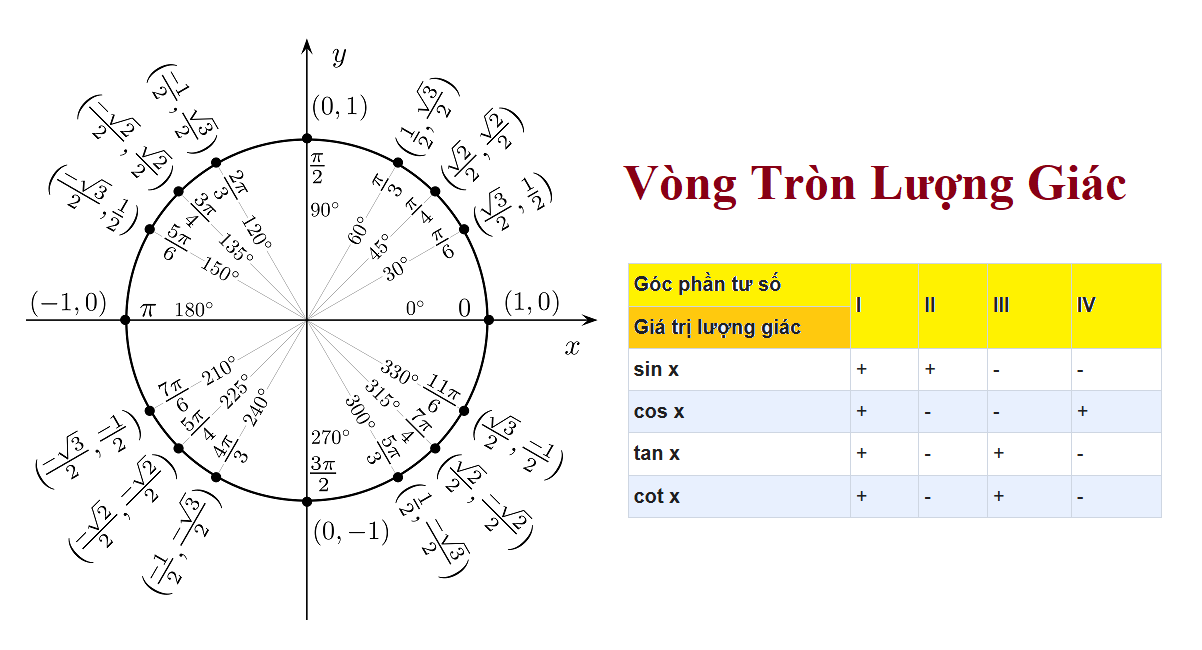
Vòng tròn lượng giác là một khái niệm quan trọng trong toán học, đặc biệt trong lĩnh vực lượng giác. Đây là công cụ trực quan và hiệu quả để giải quyết các bài toán về góc, hàm lượng giác (sin, cos, tan, cot) và mối quan hệ hình học trong mặt phẳng tọa độ. Bài viết này sẽ chia sẻ định nghĩa, tính chất và ứng dụng của vòng tròn lượng giác.
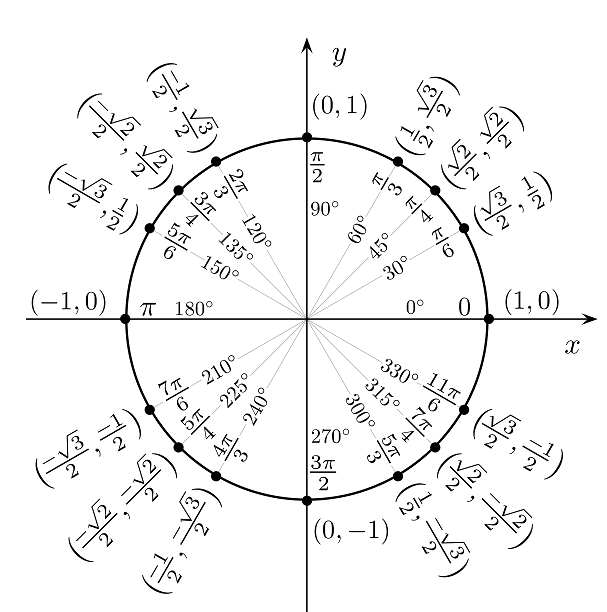
1. Khái niệm
Định nghĩa
Vòng tròn lượng giác là một vòng tròn có:
- Tâm là gốc tọa độ (0,0) trong hệ tọa độ Descartes.
- Bán kính bằng 1 đơn vị.
Vòng tròn lượng giác được sử dụng để biểu diễn các góc và giá trị của các hàm lượng giác như sin, cos, tan và cot trên mặt phẳng tọa độ.
Các yếu tố cơ bản
- Tâm của vòng tròn: Điểm O (0,0).
- Bán kính: Bán kính của vòng tròn là 1 đơn vị.
- Trục tọa độ: Trục hoành (Ox) và trục tung (Oy) chia vòng tròn thành bốn góc phần tư.
Biểu diễn góc
- Góc được đo từ trục hoành dương theo chiều ngược chiều kim đồng hồ. Góc này có thể là dương hoặc âm:
- Góc dương: Chiều ngược chiều kim đồng hồ.
- Góc âm: Chiều cùng chiều kim đồng hồ.
- Một vòng tròn đầy đủ tương ứng với 360° hoặc \(2\pi\) radian.
- Góc có thể được đo bằng độ (°) hoặc radian (rad), trong đó: \[ 180^\circ = \pi \text{ rad}. \]
2. Tính chất của vòng tròn lượng giác
Điểm đặc biệt
Vòng tròn lượng giác có các điểm đặc biệt trên trục tọa độ:
- (1, 0): Tương ứng với góc \(0^\circ\) hoặc \(0\) rad.
- (0, 1): Tương ứng với góc \(90^\circ\) hoặc \(\pi/2\) rad.
- (-1, 0): Tương ứng với góc \(180^\circ\) hoặc \(\pi\) rad.
- (0, -1): Tương ứng với góc \(270^\circ\) hoặc \(3\pi/2\) rad.
Các giá trị lượng giác của góc
Trên vòng tròn lượng giác, mỗi điểm trên vòng tròn đều liên quan đến một góc và có tọa độ \((x, y)\), trong đó:
- Giá trị cos của góc chính là hoành độ (\(x\)) của điểm.
- Giá trị sin của góc chính là tung độ (\(y\)) của điểm.
- Giá trị tan của góc được tính bằng \(\text{tan} = \frac{\text{sin}}{\text{cos}}\) (nếu \(\cos \neq 0\)).
- Giá trị cot của góc được tính bằng \(\text{cot} = \frac{\text{cos}}{\text{sin}}\) (nếu \(\sin \neq 0\)).
Góc đặc biệt
Vòng tròn lượng giác thường được sử dụng để biểu diễn các giá trị lượng giác của các góc đặc biệt:
– \(0^\circ, 30^\circ, 45^\circ, 60^\circ, 90^\circ\) (hoặc tương ứng bằng radian: \(0, \pi/6, \pi/4, \pi/3, \pi/2\)).
– Các giá trị sin, cos của các góc này thường được ghi nhớ qua bảng giá trị lượng giác cơ bản.
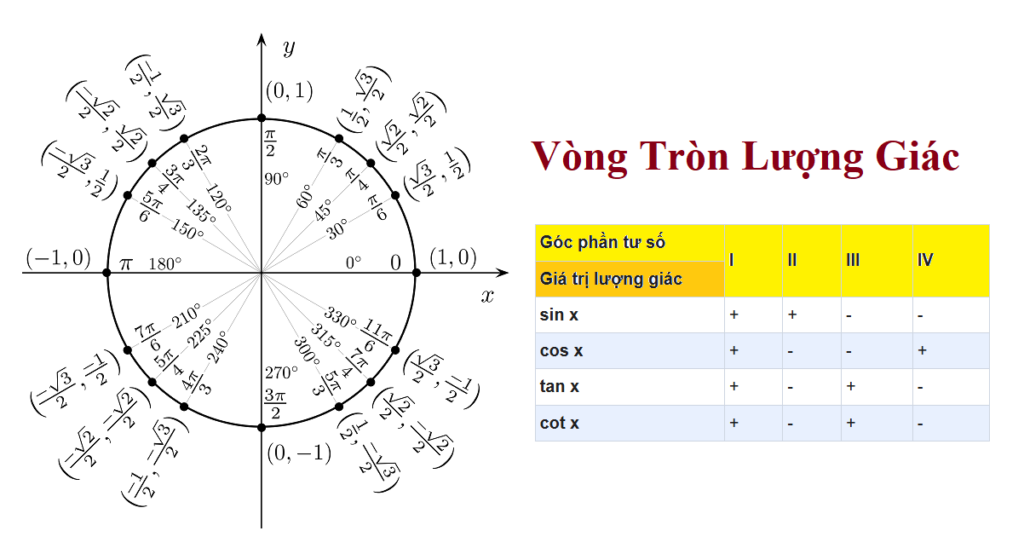
Quy luật về dấu
Trong mỗi góc phần tư, dấu của các hàm lượng giác thay đổi như sau:
- Góc phần tư I: sin, cos, tan, cot đều dương.
- Góc phần tư II: sin dương, cos và tan âm.
- Góc phần tư III: tan dương, sin và cos âm.
- Góc phần tư IV: cos dương, sin và tan âm.
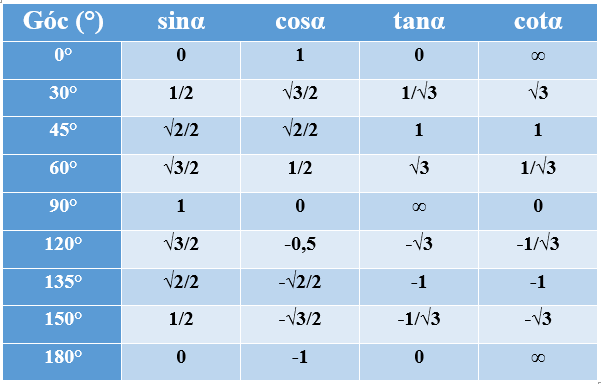
Bảng giá trị lượng giác từ 0 đến π
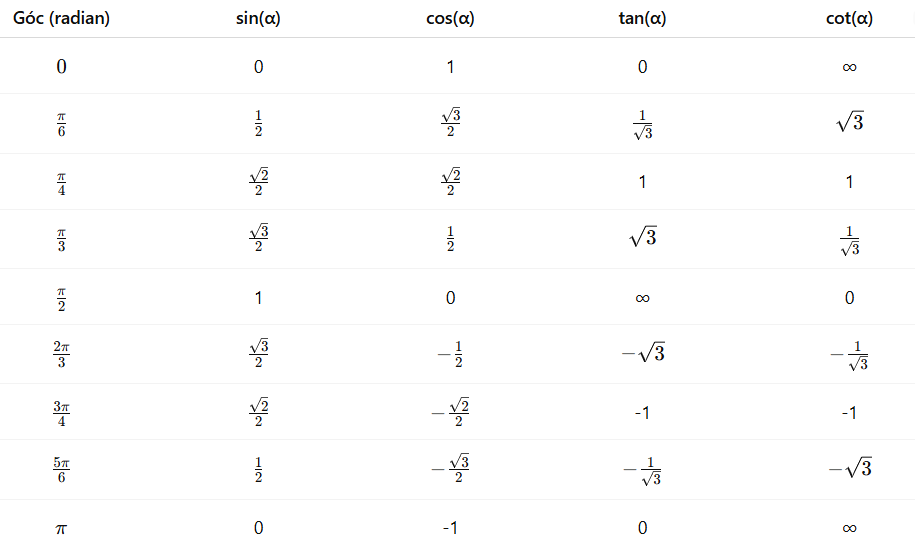
Bảng giá trị lượng giác từ 00 đến 1800
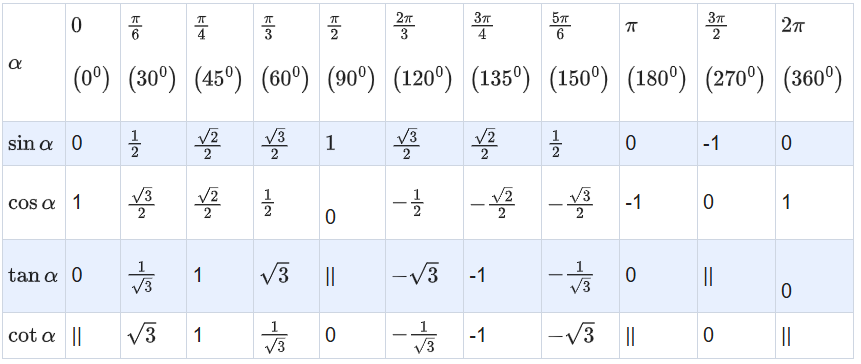
Bảng giá trị lượng giác từ 00 đến 3600
Công thức các cung liên kết trên đường tròn lượng giác
Công thức hai góc đối nhau
- cos (-x) = cos x
- sin (-x) = -sin x
- tan (-x) = -tan x
- cot (-x) = -cot x
Công thức hai góc bù nhau
- sin (π – x) = sin x
- cos (π – x) = -cos x
- tan (π – x) = -tan x
- cot (π – x) = -cot x
Công thức hai góc phụ nhau
- sin (π/2 – x) = cos x
- cos (π/2 – x) = sin x
- tan (π/2 – x) = cot x
- cot (π/2 – x) = tan x
Công thức hai góc hơn kém π
- sin (π + x) = -sin x
- cos (π + x) = -cos x
- tan (π + x) = tan x
- cot (π + x) = cot x
Công thức hai góc hơn kém π/2
- sin (π/2 + x) = cos x
- cos (π/2 + x) = -sin x
- tan (π/2 + x) = -cot x
- cot (π/2 + x) = -tan x
Dựa vào “Tính chất của vòng tròn lượng giác” đã trình bày ở trên, nếu bạn muốn ghi nhớ công thức lâu hơn và vận dụng linh hoạt khi giải các dạng bài tập liên quan, thì hãy tải ngay file bài tập bên dưới để luyện tập thường xuyên nhé!
3. Ứng dụng
Vòng tròn lượng giác trong vật lý không chỉ là một công cụ toán học, mà còn là một cách trực quan và hiệu quả để biểu diễn các hiện tượng tuần hoàn. Nó giúp kết nối các đại lượng vật lý như biên độ, pha, và tần số ….
Ví dụ 1: Một vật nhỏ dao động điều hòa trên trục Ox với biên độ 2 cm và tần số bằng 0,5 Hz. Lấy gần đúng π2 = 10. Trong một chu kì khoảng thời gian vật có vận tốc nhỏ hơn $\sqrt 2 \pi $ cm/s và gia tốc lớn hơn 10 cm/s2 bằng bao nhiêu?
Lời giải
- f = 0,5 Hz ⇒ ω = π rad/s
- A = 2 cm
- vmax = 2π cm/s
- amax = 20 cm/s2
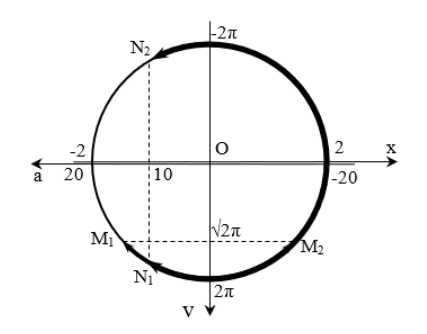
v = $\sqrt 2 \pi $ cm/s tại M ⇒ v < $\sqrt 2 \pi $ cm/s ứng với cung lớn M1M2 (không tô đậm).
a = 10 cm/s2 tại N, a > 10 cm/s2 ứng với cung nhỏ N1N2 (không tô đậm).
Cung N2M1 không tô đậm thỏa mãn cả 2 điều kiện của v và a: Δφ = 7π/12 ⇒ Δt = 7/12 s.
Ví dụ 2: Một vật dao động điều hòa theo phương trình $x = 5\cos\left(5\pi t – \frac{\pi}{3}\right)\ (cm)$ ($t$ tính bằng giây). Kể từ $t = 0$, thời điểm vật qua vị trí có ly độ $x = -2,5\ cm$ lần thứ 2017 là bao nhiêu?
Giải
Trước tiên ta biểu diễn vị trí của chất điểm ở thời điểm ban đầu trên vòng tròn (điểm $M_0$ trên Hình). Kể từ thời điểm ban đầu, mỗi khi chất điểm chuyển động tròn đi được một vòng thì hình chiếu của nó dao động được một chu kỳ và vật qua vị trí $x = -2{,}5\ cm$ hai lần, ứng với hai điểm $M_1$ và $M_2$ trên vòng tròn.
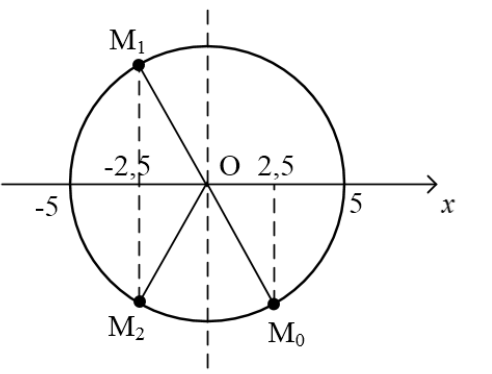
Như vậy, sau 1008 vòng, hình chiếu sẽ qua vị trí $x = -2{,}5\ \text{cm}$ 2016 lần và đã quay về đến $M_0$. Để qua được vị trí $x = -2{,}5\ \text{cm}$ lần thứ 2017, chất điểm chuyển động tròn cần đi thêm một cung tròn từ $M_0$ đến $M_1$ nữa ứng với góc quay bằng $\pi$.
Do vậy, tổng góc quay được trong quá trình chuyển động này là: $\Delta \alpha = 1008 \times 2\pi + \pi = 2017\pi.$
Thời gian tương ứng là: $\Delta t = \frac{\Delta \alpha}{\omega} = 403{,}4\ \text{s}.$
Đây chính là thời điểm cần tìm.
Nhận xét: Bài toán này có thể giải được bằng phương pháp giải phương trình lượng giác. Tuy nhiên, phương trình có rất nhiều nghiệm, sẽ làm cho người giải gặp khó khăn khi chọn nghiệm phù hợp với điều kiện bài toán.
Ví dụ 3. Hai vật dao động điều hòa trên hai đường thẳng cùng song song với trục Ox. Hình chiếu vuông góc của các vật lên trục Ox dao động với phương trình $x_1 = 10\cos\left(2{,}5\pi t + \frac{\pi}{4}\right)\ (cm)$ và $x_2 = 10\cos\left(2{,}5\pi t – \frac{\pi}{4}\right)\ (cm)$ ($t$ tính bằng giây). Kể từ $t = 0$, thời điểm hình chiếu của hai vật cách nhau $10\ cm$ lần thứ 2018 là:
Giải
Dễ dàng suy ra khoảng cách giữa hai vật có biểu thức: $d = |x_1 – x_2| = \left|10\sqrt{2}\cos\left(2{,}5\pi t + \frac{\pi}{2}\right)\right|\ (cm).$
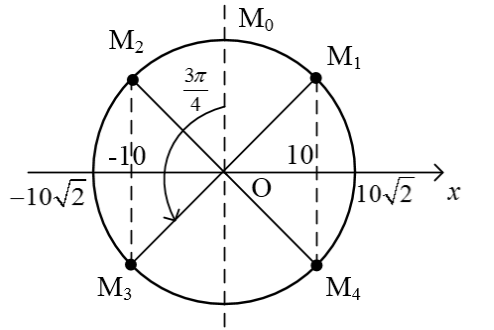
Đại lượng trong dấu giá trị tuyệt đối là một dao động điều hòa $x$. Do đó, để xác định thời điểm nó có độ lớn bằng $10\ cm$ ta dùng phương pháp vòng tròn.
Vị trí $|x| = 10\ cm$ được xác định bằng 4 điểm $M_1, M_2, M_3, M_4$ trên vòng tròn, thời điểm ban đầu được xác định bằng điểm $M_0$
Trong mỗi chu kỳ, $|x| = 10\ cm$ 4 lần ứng với 4 điểm kể trên nên sau 504 chu kỳ, khoảng cách hai vật bằng $10\ cm$ được 2016 lần, khi đó vật lại về vị trí $M_0$.
Để khoảng cách hai vật bằng $10\ cm$ lần thứ 2018, vật cần chuyển động thêm một cung tròn từ $M_0$ đến $M_3$. Tổng góc quay thực hiện trong các chuyển động này là: $\Delta \alpha = 504 \times 2\pi + \frac{3\pi}{4} = 1008{,}75\pi.$
Suy ra thời gian cần tìm là: $\Delta t = \frac{\Delta \alpha}{\omega} = 403{,}5\ (s).$
Nhận xét: Bài toán này có thể giải bằng cách tìm nghiệm của phương trình lượng giác. Tuy nhiên, trong trường hợp này, phương trình dẫn đến 4 lớp nghiệm. Do đó, người giải sẽ gặp khá nhiều khó khăn khi dò đúng nghiệm phù hợp. Việc minh họa bằng vòng tròn là có cách nhìn trực quan hơn nên dễ dàng hướng dẫn cho học sinh.
Ví dụ 4: Trên một sợi dây đàn hồi đang có sóng đứng ổn định với khoảng cách hai nút sóng liên tiếp là $6\text{cm}$. Trên dây có những phần tử sóng dao động với tần số $5\text{Hz}$ và biên độ lớn nhất là $3\text{cm}$. Gọi $N$ là vị trí một nút sóng. $C$ và $D$ là hai phần tử trên dây ở hai bên của $N$ và có vị trí cân bằng cách $N$ lần lượt là $10{,}5\text{cm}$ và $7\text{cm}$. Tại thời điểm $t_1$, phần tử $C$ có li độ $1{,}5\text{cm}$ và đang hướng về vị trí cân bằng. Vào thời điểm $t_2 = t_1 + \frac{79}{40}\text{s},$ phần tử $D$ có li độ là:
Lời giải
Biên độ của phần tử $M$ trong hiện tượng sóng dừng có biểu thức: $A_M = A_b \left| \sin\left( \frac{2\pi d}{\lambda} \right) \right|.$
Với $A_b$ là biên độ tại bụng sóng, $d$ là khoảng cách từ $M$ đến một nút bất kỳ, $\lambda$ là bước sóng trên dây. Áp dụng cho hai điểm $C$ và $D$ trên dây với khoảng cách đến nút sóng gần nhất lần lượt là dC = NC = 10,5 cm và dD = ND = 7 cm, λ = 12 cm
ta được ${A_C} = 1,5\sqrt 2 {\rm{ (cm)}}$ và ${A_D} = 1,5{\rm{ (cm)}}$.
Dao động của hai phần tử $C$ và $D$ được biểu diễn bằng hai chuyển động tròn đều có bán kính quỹ đạo khác nhau (Hình vẽ). Vị trí của phần tử $C$ tại thời điểm $t_1$ được xác định bằng điểm $C_1$ trên vòng tròn. Ở thời điểm $t_2$, phần tử $C$ được xác định bằng điểm $C_2$ trên vòng tròn, cách $C_1$ một góc quay bằng $\omega \Delta t = 19\pi + \frac{3\pi}{4}.$
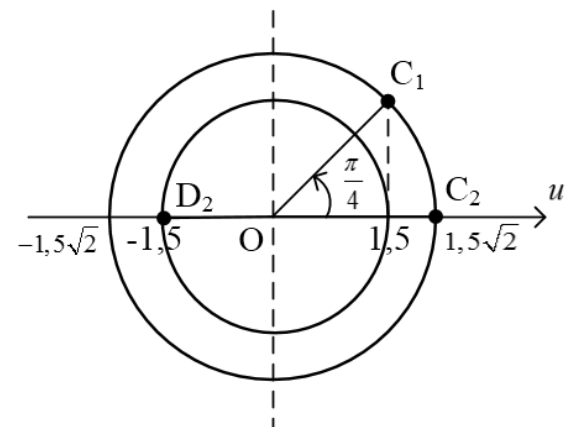
Ta đã biết, trong hiện tượng sóng dừng, những phần tử thuộc hai bó sóng kề nhau luôn dao động ngược pha nhau. Dựa vào các khoảng cách từ $C$ và $D$ đến nút $N$ và khoảng cách giữa hai nút sóng kề nhau, ta dễ dàng suy ra hai phần tử này thuộc hai bó sóng dao động ngược pha nhau.
Do đó, ở thời điểm $t_2$, phần tử tại $D$ được xác định bằng vị trí $D_2$ trên vòng tròn (ngược pha với $C_2$, cách $C_2$ một góc quay bằng $\pi$).
Điểm này có ly độ bằng $-1{,}5\text{cm}$. Chọn đáp án A.
Nhận xét: Nếu không sử dụng phương pháp vòng tròn sẽ rất khó xác định được ly độ của phần tử $D$ vì ở đây có đến hai nguyên nhân dẫn đến sự lệch pha trong dao động của hai phần tử $C$ và $D$ (thời gian và khoảng cách).
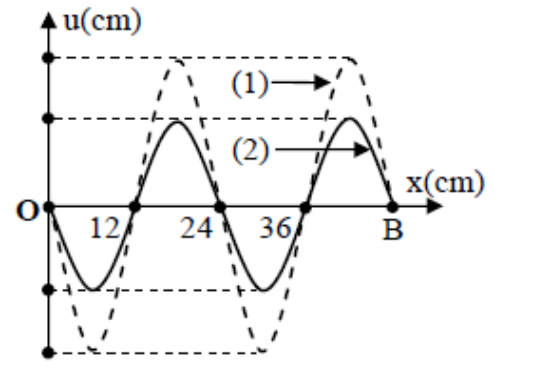
Ví dụ 5: Trên một sợi dây $OB$ căng ngang, hai đầu cố định đang có sóng dừng với tần số sóng $f$ xác định. Gọi $M, N, P$ là ba điểm trên dây có vị trí cân bằng cách $B$ lần lượt là $4\text{cm}$, $6\text{cm}$ và $38\text{cm}$. Hình vẽ mô tả hình dạng sợi dây tại thời điểm $t_1$ (đường 1) và $t_2 = t_1 + \frac{11}{12f}$ (đường 2). Tại thời điểm $t_1$, ly độ của phần tử dây ở $N$ bằng biên độ của phần tử dây ở $M$ và tốc độ của phần tử dây ở $M$ là $60\text{cm/s}$. Tại thời điểm $t_2$, vận tốc của phần tử dây ở $P$ là bao nhiêu?
Phân tích đề:
Đây là loại bài toán có liên quan đến đồ thị nên cần phải khai thác triệt để dữ kiện từ hình vẽ.
Từ hình dạng sợi dây đã cho, ta có thể xác định được bước sóng của sóng trên dây. Dựa vào các khoảng cách từ $M$, $N$, $P$ đến $B$, ta có thể suy ra biên độ dao động của các điểm này (tính theo biên độ của điểm bụng) và quan hệ về pha giữa chúng.
Từ quan hệ về ly độ của $N$ và biên độ của $M$, tốc độ của $M$ ở thời điểm $t_1$, ta xác định được biên độ tại $M$, $N$ bằng phương pháp vòng tròn rồi suy ra biên độ tại $P$.
Cuối cùng, dùng khoảng thời gian giữa thời điểm $t_1$ đến thời điểm $t_2$, cùng với quan hệ về pha sẽ xác định được ly độ và tốc độ của $P$ (bằng phương pháp vòng tròn).
Lời giải
Hình cho ta giá trị bước sóng $\lambda = 24,(\text{cm})$.
Sử dụng công thức biên độ sóng dừng $A = {A_b}\left| {\sin \left( {\frac{{2\pi d}}{\lambda }} \right)} \right|\quad $ với ${A_b}$ là biên độ tại bụng sóng.
ta tìm được biên độ sóng tại các điểm $M, N, P$ lần lượt là ${A_M} = \frac{{{A_b}\sqrt 3 }}{2},$ ${A_N} = {A_b},$ ${A_P} = \frac{{{A_b}}}{2}.$
Từ các khoảng cách từ $M, N, P$ đến đầu $B$, ta suy ra $N$ dao động cùng pha với $M$ còn $P$ dao động ngược pha với $M$.
Tại thời điểm $t_1$, ly độ của $N$ bằng biên độ của $M$ nên được biểu diễn bằng điểm $N_1$, $M$ được biểu diễn bằng điểm $M_1$ trên Hình 7. Dễ thấy $M_1 O A_b = \frac{\pi}{6}$
nên ly độ của $M$ lúc này bằng $\frac{A_M \sqrt{3}}{2}.$
Sử dụng hệ thức độc lập với thời gian, sẽ được tốc độ tại $M$ lúc này bằng một nửa tốc độ cực đại của $M$: $|{v_M}| = \frac{1}{2}\omega {A_M}$ $ = \frac{{\pi \sqrt 3 }}{2}{A_b}$ $ = \frac{{40\sqrt 3 }}{\pi }({\rm{cm/s}}).$
Góc quay được trong khoảng thời gian từ thời điểm $t_1$ đến thời điểm $t_2$ là $\Delta \alpha = \omega \Delta t = \frac{11\pi}{6}.$
Tại thời điểm này, điểm $N_2$ có vị trí được xác định bằng $P_2$ (P ngược pha với N) có ly độ bằng $-\frac{A_b}{2}.$
Hệ thức độc lập với thời gian cho ta tốc độ của $P$ bằng $|v_P| = \omega A_P \sqrt{3} = 60(\text{cm/s}).$
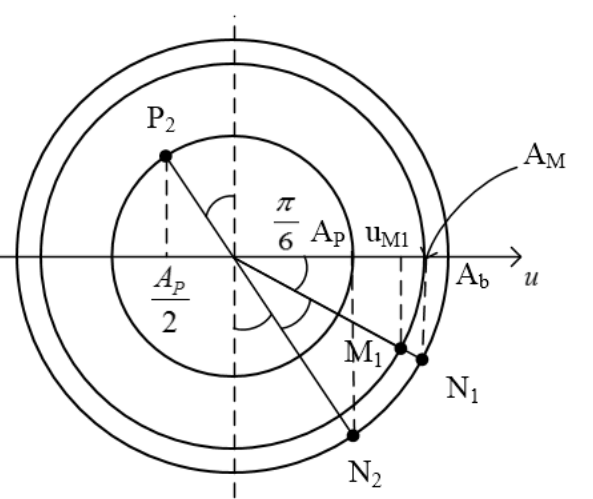
Hình trên cho thấy, tại thời điểm $t_2$, điểm $P$ có vận tốc âm (đang chuyển động ngược chiều dương).
Nhận xét: Phương pháp vòng tròn giúp ta xác định được vị trí của chất điểm dao động điều hòa trong hiện tượng sóng dừng một cách nhanh chóng, dựa vào khoảng thời gian, góc quay và độ lệch pha giữa các điểm.
Trong ví dụ này, có thể nói rằng chỉ có phương pháp vòng tròn có thể dẫn đến kết quả nhanh và chính xác.
Dựa trên các ví dụ vừa phân tích, ta có thể thấy rõ phương pháp vòng tròn lượng giác là một công cụ vô cùng hiệu quả khi giải các bài tập dao động trong vật lý. Phương pháp này không chỉ giúp hình dung trực quan hơn mà còn rút ngắn thời gian tìm lời giải chính xác. Nếu bạn muốn luyện tập thêm kỹ năng vận dụng vòng tròn lượng giác, hãy truy cập ngay trang Siêu Giỏi và tải ngay bộ bài tập vật lý chuyên đề dưới đây để thực hành nhé!
4. Câu hỏi thường gặp
1. Vòng tròn lượng giác là gì và dùng để làm gì trong lượng giác học?
Vòng tròn lượng giác (hay đường tròn đơn vị) là đường tròn có bán kính 1, tâm tại gốc tọa độ. Nó giúp biểu diễn giá trị của các hàm lượng giác như $\sin \alpha$ và $\cos \alpha$ bằng tọa độ điểm tương ứng trên trục $x$ và $y$.
2. Làm thế nào để vẽ đúng vòng tròn lượng giác trong mặt phẳng tọa độ Oxy?
Bạn vẽ một đường tròn tâm O(0;0), bán kính bằng 1 đơn vị, kẻ hai trục vuông góc Ox và Oy. Trục Ox biểu diễn $\cos \alpha$, còn Oy biểu diễn $\sin \alpha$.
3. Bảng giá trị lượng giác đặc biệt được xây dựng dựa trên nguyên tắc nào?
Các giá trị trong bảng được tính từ tọa độ điểm tương ứng trên đường tròn đơn vị, như: $ \sin 30^\circ = \frac{1}{2}, \quad \cos 30^\circ = \frac{\sqrt{3}}{2}. $
4. Làm sao xác định sin và cos của một góc bất kỳ trên đường tròn đơn vị?
Lấy điểm M trên đường tròn sao cho cung $\widehat{AM} = \alpha$. Khi đó: $ \sin \alpha = y_M, \quad \cos \alpha = x_M. $
5. Dấu của các hàm lượng giác thay đổi thế nào trong từng góc phần tư?
Góc phần tư I: tất cả đều dương.
Góc phần tư II: chỉ $\sin$ dương.
Góc phần tư III: chỉ $\tan$ dương.
Góc phần tư IV: chỉ $\cos$ dương.
6. Làm thế nào để xác định đơn vị radian trên đường tròn đơn vị?
Radian được tính theo độ dài cung, với công thức: $ 1\ \text{radian} = \frac{180^\circ}{\pi}. $
7. Có cách nào học thuộc vòng tròn lượng giác nhanh không?
Bạn nên học theo nhóm góc đặc biệt (0°, 30°, 45°, 60°, 90°) và ghi nhớ tọa độ: $ (\cos \alpha, \sin \alpha) = \left(\frac{\sqrt{3}}{2}, \frac{1}{2}\right) \text{ tại } 30^\circ. $
8. Vòng tròn lượng giác giúp giải phương trình lượng giác như thế nào?
Nhờ vị trí đối xứng của điểm M trên đường tròn, ta có thể suy ra các nghiệm của hàm $\sin x$, $\cos x$, hoặc $\tan x$ dựa trên tính tuần hoàn của góc.
9. Khi chuyển từ độ sang radian cần dùng công thức gì?
Sử dụng: $ \alpha_{\text{radian}} = \alpha_{\text{degree}} \times \frac{\pi}{180}. $
10. Mối liên hệ giữa đường tròn đơn vị và đồ thị hàm số sin là gì?
Khi điểm M di chuyển trên đường tròn, tung độ $y = \sin \alpha$ tạo thành đồ thị hình sin tuần hoàn.
11. Tại sao cần nắm rõ giá trị của các góc đặc biệt trên đường tròn?
Vì các góc như $0^\circ, 30^\circ, 45^\circ, 60^\circ, 90^\circ$ là nền tảng để suy ra mọi giá trị khác bằng các công thức cộng, trừ, nhân đôi góc.
12. Làm sao xác định góc bù và góc đối trên đường tròn?
Nếu $\alpha$ là một góc, thì: $ \sin(\pi – \alpha) = \sin \alpha, \quad \cos(\pi – \alpha) = -\cos \alpha. $
13. Có thể dùng vòng tròn lượng giác để tính giá trị của tan và cot không?
Có. Dựa trên: $ \tan \alpha = \frac{\sin \alpha}{\cos \alpha}, \quad \cot \alpha = \frac{\cos \alpha}{\sin \alpha}. $
14. Vòng tròn lượng giác có ứng dụng gì trong Vật lý?
Trong dao động điều hòa, vị trí của vật dao động có thể biểu diễn bằng chuyển động tròn đều trên đường tròn đơn vị: $ x = A\cos(\omega t + \varphi). $
15. Tại sao trục Ox và Oy lại được chọn cho cos và sin?
Vì trong tam giác vuông đơn vị, cạnh kề ứng với $\cos \alpha$ nằm trên trục Ox, còn cạnh đối ứng với $\sin \alpha$ nằm trên Oy.
16. Làm sao xác định góc quay ngược chiều kim đồng hồ trong lượng giác?
Chiều dương của góc được quy ước ngược chiều kim đồng hồ; góc âm quay theo chiều ngược lại.
17. Khi nào giá trị sin hoặc cos bằng 0 hoặc ±1?
$\sin \alpha = 0$ khi $\alpha = 0, \pi, 2\pi.$
$\cos \alpha = 0$ khi $\alpha = \frac{\pi}{2}, \frac{3\pi}{2}.$
$\sin \alpha = 1$ tại $\alpha = \frac{\pi}{2}.$
18. Làm sao nhận biết hai góc có cùng giá trị lượng giác?
Nếu $\alpha$ và $\beta$ đồng vị trên đường tròn (chênh lệch bội của $2\pi$), ta có: $ \sin \alpha = \sin \beta, \quad \cos \alpha = \cos \beta. $
19. Có công thức nào liên hệ giữa sin² và cos² không?
Công thức cơ bản trên đường tròn đơn vị là: $ \sin^2 \alpha + \cos^2 \alpha = 1. $
Vòng tròn lượng giác là công cụ trực quan và hiệu quả để nghiên cứu hàm lượng giác, giải bài toán về góc và đo đạc trong mặt phẳng tọa độ. Để nắm vững, học sinh cần rèn tư duy hình học, ghi nhớ giá trị cơ bản và áp dụng vào thực tế.