Trong Toán học, đặc biệt ở phần lượng giác, việc hiểu rõ liên hệ giữa độ và radian là vô cùng quan trọng. Hai đơn vị này đều dùng để đo góc phẳng, nhưng radian thường được sử dụng trong các công thức lượng giác, đạo hàm hay vật lý. Nếu bạn biết cách quy đổi linh hoạt giữa chúng, bạn sẽ dễ dàng giải quyết các bài toán về cung tròn, chu kỳ hay hàm lượng giác một cách chính xác và nhanh chóng.
Bài viết này sẽ giúp bạn nắm chắc khái niệm, công thức và ví dụ thực tế về độ – radian, cùng với các mẹo học nhanh dễ nhớ.
1. Khái niệm độ và radian
Độ là gì?
Độ là đơn vị đo thông thường của góc trong hình học. Một vòng tròn được chia thành $360^\circ$, mỗi độ lại chia thành $60’$ (phút) và mỗi phút chia thành $60”$ (giây).
Ví dụ: $37^\circ45’30”$ nghĩa là 37 độ, 45 phút và 30 giây.
Radian là gì?
Radian (ký hiệu rad) là đơn vị đo góc trong hệ SI, được định nghĩa dựa trên độ dài cung tròn.
Nếu một cung tròn có độ dài bằng đúng bán kính của đường tròn, thì góc chắn cung đó có số đo bằng 1 radian.
Công thức liên hệ giữa độ dài cung và radian là: $l = R \cdot \alpha$
Trong đó:
- $l$ là độ dài cung tròn,
- $R$ là bán kính,
- $\alpha$ là góc ở tâm (đo bằng radian).
Tại sao cần dùng radian?
Radian giúp các công thức lượng giác và đạo hàm trở nên đơn giản hơn. Ví dụ:
$\frac{d}{dx}(\sin x) = \cos x$ chỉ đúng khi $x$ tính theo radian.
Do đó, radian là đơn vị chuẩn trong các bài toán giải tích và vật lý.
2. Công thức chuyển đổi giữa độ và radian
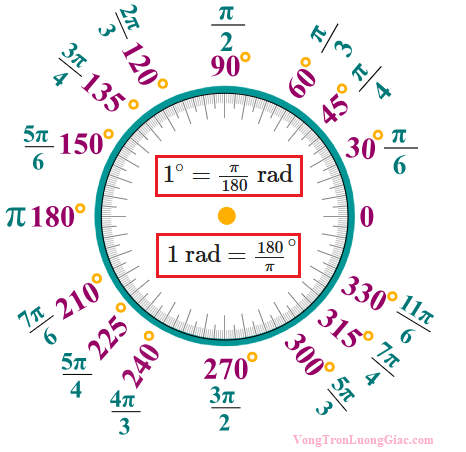
Từ độ sang radian
$1^\circ = \frac{\pi}{180} \text{ rad}$
Hay nói cách khác, $x^\circ = x \cdot \frac{\pi}{180}$
Từ radian sang độ
$1 \text{ rad} = \frac{180}{\pi}^\circ$
Suy ra: $x \text{ rad} = x \cdot \frac{180}{\pi}^\circ$
Ghi nhớ nhanh:
180∘ = π rad và 360∘ = 2π rad.
3. Ví dụ minh họa có lời giải
Ví dụ 1: Đổi từ độ sang radian
Hãy đổi các góc sau sang radian: $72^\circ; 600^\circ; -37^\circ45’30”.$
Lời giải:
$72^\circ = 72 \cdot \frac{\pi}{180} = \frac{2\pi}{5}$
$600^\circ = 600 \cdot \frac{\pi}{180} = \frac{10\pi}{3}$
$ – {37^0}45’30”$ $ = – {37^0} – {\frac{{45}}{{60}}^0} – \frac{{{{30}^0}}}{{3600}}$ $ = – {\frac{{4531}}{{120}}^0}$ $ = – \frac{{4531\pi }}{{21600}}$ $ \approx – 0,6587{\rm{ rad}}.$
Ví dụ 2: Đổi từ radian sang độ
Hãy đổi các góc sau ra độ: $\frac{5\pi}{18}; \frac{3\pi}{5}; -4.$
Lời giải:
$\frac{5\pi}{18} = \frac{5\pi}{18} \cdot \frac{180}{\pi} = 50^\circ$
$\frac{3\pi}{5} = \frac{3\pi}{5} \cdot \frac{180}{\pi} = 108^\circ$
$-4 = -4 \cdot \frac{180}{\pi} \approx -229^\circ$
Ví dụ 3: Bài tập nâng cao tổng hợp
Đổi các góc sau: ${54^0};$ ${30^0}45′;$ $ – {60^0};$ $ – {210^0};$ $\frac{\pi }{5};$ $ – \frac{{5\pi }}{6};$ $\frac{{4\pi }}{3};$ $3,56\pi .$
Giải tương tự theo công thức trên, kết quả lần lượt:
$\frac{{3\pi }}{{10}};$ $\frac{{41\pi }}{{240}};$ $ – \frac{\pi }{3};$ $ – \frac{{7\pi }}{6};$ ${36^0};$ $ – {150^0};$ ${240^0};$ ${640^0}48′.$
4. Mẹo học nhanh và ghi nhớ công thức
Khi đổi từ độ sang radian, nhân với $\frac{\pi}{180}.$
Khi đổi từ radian sang độ, nhân với $\frac{180}{\pi}.$
Một số giá trị góc thường gặp cần thuộc lòng:
- $\frac{\pi}{6} = 30^\circ$
- $\frac{\pi}{4} = 45^\circ$
- $\frac{\pi}{3} = 60^\circ$
- $\pi = 180^\circ$
- $2\pi = 360^\circ$
Mẹo nhớ: chỉ cần nhớ “π ứng với 180°”, mọi phép đổi đều suy ra được ngay.
5. Bài tập
Bài tập 1. Đổi số đo của các góc sau ra radian: $72^\circ; 600^\circ; -37^\circ45’30”.$
Lời giải
Vì $1^\circ = \frac{\pi}{180} \text{ rad}$ nên
$72^\circ = 72 \cdot \frac{\pi}{180} = \frac{2\pi}{5};$
$600^\circ = 600 \cdot \frac{\pi}{180} = \frac{10\pi}{3};$
$-37^\circ45’30” = -37^\circ – \left( \frac{45}{60} \right)^\circ – \left( \frac{30}{60 \cdot 60} \right)^\circ = \left( \frac{4531}{120} \right)^\circ = \frac{4531}{120} \cdot \frac{\pi}{180} \approx 0{,}6587.$
Bài tập 2. Đổi số đo của các góc sau ra độ: $\frac{5\pi}{18}; \frac{3\pi}{5}; -4.$
Lời giải
Vì $1 \text{ rad} = \left( \frac{180}{\pi} \right)^\circ$ nên
$\frac{5\pi}{18} = \frac{5\pi}{18} \cdot \frac{180}{\pi} = 50^\circ;$
$\frac{3\pi}{5} = \frac{3\pi}{5} \cdot \frac{180}{\pi} = 108^\circ;$
$-4 = -4 \cdot \frac{180}{\pi} \approx -226^\circ48′.$
Bài tập 3. Đổi số đo của các góc sau ra radian: $54^\circ; 30^\circ45′; -60^\circ; -210^\circ.$
Lời giải
$54^\circ = 54 \cdot \frac{\pi}{180} = \frac{3\pi}{10};$
$30^\circ45′ = 30^\circ + \left( \frac{45}{60} \right)^\circ = \left( \frac{123}{4} \right)^\circ = \frac{123}{4} \cdot \frac{\pi}{180} = \frac{41\pi}{240} \approx 0{,}5367;$
$-60^\circ = -60 \cdot \frac{\pi}{180} = -\frac{\pi}{3};$
$-210^\circ = -210 \cdot \frac{\pi}{180} = -\frac{7\pi}{6}.$
Bài tập 4. Đổi số đo của các góc sau ra độ: $\frac{\pi}{5}; -\frac{5\pi}{6}; \frac{4\pi}{3}; 3{,}56\pi.$
Lời giải
$\frac{\pi}{5} = \left( \frac{\pi}{5} \cdot \frac{180}{\pi} \right)^\circ = 36^\circ;$
$-\frac{5\pi}{6} = -\left( \frac{5\pi}{6} \cdot \frac{180}{\pi} \right)^\circ = -150^\circ;$
$\frac{4\pi}{3} = \left( \frac{4\pi}{3} \cdot \frac{180}{\pi} \right)^\circ = 240^\circ;$
$3{,}56\pi = \left( 3{,}56\pi \cdot \frac{180}{\pi} \right)^\circ \approx 640^\circ48′.$
6. Ứng dụng thực tế của radian và độ
- Trong vật lý: đo dao động, chuyển động tròn, tính tốc độ góc $\omega = \frac{\Delta \alpha}{\Delta t}$.
- Trong toán học: tính cung tròn $l = R \cdot \alpha$ và diện tích quạt tròn $S = \frac{1}{2}R^2\alpha$.
- Trong kỹ thuật: đo góc quay của bánh răng, cánh quạt, động cơ, robot công nghiệp.
Nhờ việc chuyển đổi linh hoạt giữa độ và radian, các công thức này trở nên dễ hiểu và chính xác hơn.
7. FAQs
1. Radian được ứng dụng như thế nào trong chuyển động tròn và lượng giác?
Trả lời:
Trong chuyển động tròn đều, radian giúp tính các đại lượng một cách chính xác:
Độ dài cung tròn: $l = R \cdot \alpha$
Tốc độ góc: $\omega = \frac{\Delta \alpha}{\Delta t}$
Chu kỳ quay: $T = \frac{2\pi}{\omega}$
Trong lượng giác, radian là cơ sở để định nghĩa hàm sin, cos, tan. Các công thức đạo hàm như:
$\frac{d}{dx}(\sin x) = \cos x, \quad \frac{d}{dx}(\cos x) = -\sin x$
chỉ đúng khi $x$ tính bằng radian.
Vì vậy, khi học chương “Hàm lượng giác” hoặc “Đạo hàm của hàm lượng giác”, hãy luôn quy đổi góc về radian để tránh sai kết quả.
2. Có những bài tập đổi độ sang radian nào thường gặp trong lớp 10?
Trả lời:
Một số bài tập cơ bản thường gặp:
$30^\circ = 30 \cdot \frac{\pi}{180} = \frac{\pi}{6}$
$45^\circ = 45 \cdot \frac{\pi}{180} = \frac{\pi}{4}$
$150^\circ = 150 \cdot \frac{\pi}{180} = \frac{5\pi}{6}$
$300^\circ = 300 \cdot \frac{\pi}{180} = \frac{5\pi}{3}$
Bài nâng cao: ${37^0}45’$ $ = {37,75^0}$ $ = 37,75 \cdot \frac{\pi }{{180}}$ $ \approx 0,659{\rm{ rad}}$
Học sinh nên luyện đổi qua lại thật nhiều để làm quen với dạng đề thi trắc nghiệm.
3. Cách đổi radian sang độ bằng công thức nhanh nhất là gì?
Trả lời:
Khi đổi radian → độ, chỉ cần nhân với $\frac{180}{\pi}$.
Cách nhớ nhanh: “Radian nhân 180, chia π”.
Ví dụ: $\frac{{3\pi }}{5}{\rm{ rad}}$ $ = \frac{{3\pi }}{5} \cdot \frac{{180}}{\pi }$ $ = {108^0}$
Nếu sử dụng máy tính, bạn có thể nhập trực tiếp giá trị radian rồi nhân với $180 / \pi$ để ra số đo theo độ trong vài giây.
4. Công thức chuyển đổi giữa độ và radian có ví dụ minh họa là gì?
Trả lời:
Công thức cơ bản để chuyển đổi là:
Từ độ sang radian: $x^\circ = x \cdot \frac{\pi}{180}$
Từ radian sang độ: $x \text{ rad} = x \cdot \frac{180}{\pi}^\circ$
Ví dụ:
$60^\circ = 60 \cdot \frac{\pi}{180} = \frac{\pi}{3} \text{ rad}$
$\frac{\pi}{4} \text{ rad} = \frac{\pi}{4} \cdot \frac{180}{\pi} = 45^\circ$
Hai công thức này luôn là nền tảng cho mọi bài toán lượng giác.
8. Kết luận
Qua bài học này, bạn đã nắm được:
- Hai đơn vị đo góc cơ bản là độ và radian,
- Công thức chuyển đổi qua lại nhanh chóng,
- Ví dụ và bài tập minh họa chi tiết để luyện tập.
Hãy ghi nhớ công thức cơ bản: ${x^0} = x \cdot \frac{\pi }{{180}}$ và $x{\rm{ rad}} = x \cdot {\frac{{180}}{\pi }^0}.$
Đây là bước khởi đầu quan trọng để bạn học tốt các phần tiếp theo như cung tròn, hàm lượng giác, đồ thị sin – cos, hay công thức lượng giác nâng cao.