Khi học lượng giác, việc xác định dấu của các giá trị lượng giác là bước nền tảng quan trọng giúp bạn tính toán nhanh và chính xác trong các bài toán về phương trình, bất đẳng thức, hoặc biến đổi lượng giác.

Hiểu đơn giản, “dấu” của các hàm $\sin, \cos, \tan$ cho biết giá trị của chúng dương hay âm tại một vị trí góc nhất định trên đường tròn lượng giác.

Việc nắm rõ quy tắc này giúp bạn tránh nhầm lẫn khi làm bài thi, đặc biệt trong các dạng như “rút gọn biểu thức lượng giác” hay “tính giá trị hàm tại góc lớn hơn $2\pi$”.

1. Kiến thức nền tảng

Trên mặt phẳng tọa độ, đường tròn lượng giác là đường tròn tâm $O(0,0)$ bán kính bằng 1.

Một góc lượng giác $\alpha$ được biểu diễn bằng cung $\overset{\frown}{AM}$ sao cho: A(1, 0), M(cosα, sinα)

Tức là:

• Hoành độ của $M$ chính là $\cos\alpha$
• Tung độ của $M$ chính là $\sin\alpha$

Từ đó, ta có thể xác định dấu của các hàm lượng giác dựa vào vị trí của điểm $M$ trên mặt phẳng.

2. Dấu của các giá trị lượng giác theo góc phần tư

Mặt phẳng được chia thành 4 góc phần tư (ký hiệu I, II, III, IV).

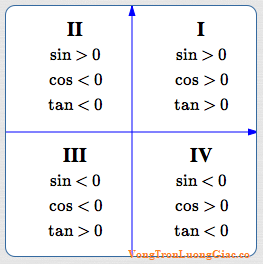
Mỗi góc phần tư sẽ quyết định dấu của các giá trị lượng giác như sau:

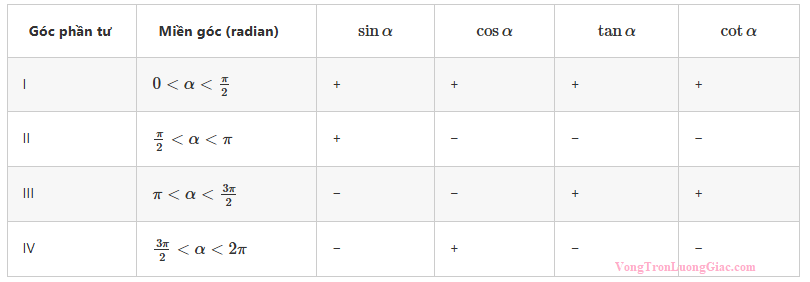
Quy tắc nhớ nhanh: “Sin dương góc I, II — Cos dương góc I, IV — Tan dương góc I, III.”

3. Cách xác định dấu khi góc lớn hoặc âm

Nếu góc $\alpha$ không nằm trong khoảng $[0, 2\pi)$, ta cần rút gọn góc bằng cách trừ hoặc cộng bội của $2\pi$:

$\alpha’ = \alpha + k \cdot 2\pi$ với $k \in \mathbb{Z}$

Vì các hàm lượng giác có chu kỳ nên:

• $\sin(\alpha + 2\pi) = \sin\alpha$
• $\cos(\alpha + 2\pi) = \cos\alpha$
• $\tan(\alpha + \pi) = \tan\alpha$

Sau khi đưa góc về khoảng $[0, 2\pi)$, ta xác định góc phần tư của nó và dựa vào bảng dấu trên để suy ra dấu của các giá trị lượng giác.

4. Một số công thức chuyển đổi thường gặp

Các góc đối xứng giúp bạn nhanh chóng suy luận dấu:

• $\sin(\pi – \alpha) = \sin\alpha$ (cùng dấu, vì cùng tung độ)
• $\cos(\pi – \alpha) = -\cos\alpha$ (đối xứng qua trục tung)
• $\sin(-\alpha) = -\sin\alpha$
• $\cos(-\alpha) = \cos\alpha$
• $\tan(-\alpha) = -\tan\alpha$

Những công thức này thường dùng để xác định dấu khi gặp góc âm hoặc góc bù, góc đối.

5. Ví dụ

Ví dụ 1: Xác định dấu của $\sin\left(\frac{5\pi}{6}\right)$

Giải

$\frac{5\pi}{6} = \pi – \frac{\pi}{6}$ → thuộc góc phần tư thứ II.

Theo bảng dấu: $\sin$ dương ở góc phần tư II.

Kết luận: $\sin\left(\frac{5\pi}{6}\right) > 0$

Ví dụ 2: Xác định dấu của $\tan\left(-\frac{3\pi}{4}\right)$

Giải

Góc $-\frac{3\pi}{4}$ tương đương với $\frac{5\pi}{4}$ (cộng thêm $2\pi$).

Góc này nằm ở góc phần tư III, nơi $\tan > 0$.

Kết luận: $\tan\left(-\frac{3\pi}{4}\right) > 0$

Ví dụ 3: Tính dấu của biểu thức $\cot\frac{2\pi}{3} \cdot \sin\left(-\frac{2\pi}{3}\right)$

Giải

$\cot\frac{2\pi}{3}$ thuộc góc phần tư II → $\cot < 0$

$\sin\left(-\frac{2\pi}{3}\right) = -\sin\frac{2\pi}{3}$ → $\sin\frac{2\pi}{3} > 0$ (góc phần tư II) → $\sin(-\frac{2\pi}{3}) < 0$

Suy ra tích của hai giá trị âm: $(-) \times (-) = (+)$

👉 Kết luận: Biểu thức dương.

Ví dụ 4. Xác định dấu các biểu thức:

a) $A = \sin 50^\circ \cdot \cos(-100^\circ)$

b) $B = \sin 195^\circ \cdot \tan \frac{20\pi}{7}$

Giải

a) $A = \sin 50^\circ \cdot \cos(-100^\circ)$

Ta có: điểm cuối của cung $50^\circ$ thuộc góc phần tư thứ I nên $\sin 50^\circ > 0$.

Điểm cuối của cung $-100^\circ$ thuộc góc phần tư thứ III nên $\cos(-100^\circ) < 0$.

Do đó, $A < 0$.

b) $B = \sin 195^\circ \cdot \tan \frac{20\pi}{7}$

Ta có: điểm cuối của cung $195^\circ$ thuộc góc phần tư thứ III nên $\sin 195^\circ < 0$.

Điểm cuối của cung $\frac{20\pi}{7} = \frac{6\pi}{7} + 2\pi$ thuộc góc phần tư thứ II nên $\tan \frac{20\pi}{7} < 0$.

Do đó, $B > 0$.

Ví dụ 5. Xác định dấu các biểu thức:

a) $A = \cot \frac{2\pi}{5} \cdot \sin \left( -\frac{2\pi}{3} \right)$

b) $B = \cos \frac{4\pi}{5} \cdot \sin \frac{\pi}{3} \cdot \tan \frac{4\pi}{3} \cdot \cot \frac{9\pi}{5}$

Giải

a) $A = \cot \frac{2\pi}{5} \cdot \sin \left( -\frac{2\pi}{3} \right)$

Ta có: điểm cuối của cung $\frac{2\pi}{5}$ thuộc góc phần tư thứ I nên $\cot \frac{2\pi}{5} > 0$.

Điểm cuối của cung $-\frac{2\pi}{3}$ thuộc góc phần tư thứ III nên $\sin \left( -\frac{2\pi}{3} \right) < 0$.

Do đó, $A < 0$.

b) $B = \cos \frac{4\pi}{5} \cdot \sin \frac{\pi}{3} \cdot \tan \frac{4\pi}{3} \cdot \cot \frac{9\pi}{5}$

Ta có: điểm cuối của cung $\frac{4\pi}{5}$ thuộc góc phần tư thứ II nên $\cos \frac{4\pi}{5} < 0$.

Điểm cuối của cung $\frac{\pi}{3}$ thuộc góc phần tư thứ I nên $\sin \frac{\pi}{3} > 0$.

Điểm cuối của cung $\frac{4\pi}{3}$ thuộc góc phần tư thứ III nên $\tan \frac{4\pi}{3} > 0$.

Điểm cuối của cung $\frac{9\pi}{5} = -\frac{\pi}{5} + 2\pi$ thuộc góc phần tư thứ IV nên $\cot \frac{9\pi}{5} < 0$.

Do đó, $B > 0$.

Ví dụ 6. Cho $\pi < \alpha < \frac{3\pi}{2}.$ Xét dấu các biểu thức sau:

a) $A = \cos \left( \alpha – \frac{\pi}{2} \right).$

b) $B = \tan \left( \frac{2019\pi}{2} – \alpha \right).$

Giải

a) $A = \cos \left( \alpha – \frac{\pi}{2} \right) = \cos \left( \frac{\pi}{2} – \alpha \right) = \sin \alpha < 0.$

b) $B = \tan \left( \frac{2019\pi}{2} – \alpha \right) = \tan \left( \frac{\pi}{2} – \alpha + 1009\pi \right) = \tan \left( \frac{\pi}{2} – \alpha \right) = \cot \alpha > 0.$

Ví dụ 7. Xác định dấu của $\sin \alpha, \cos \alpha, \tan \alpha,$ biết:

a) $\frac{3\pi}{2} < \alpha < \frac{7\pi}{4}.$

b) $3\pi < \alpha < \frac{10\pi}{3}.$

c) $\frac{5\pi}{2} < \alpha < \frac{11\pi}{4}.$

Giải

a) $\frac{3\pi}{2} < \alpha < \frac{7\pi}{4}.$

Ta có: điểm cuối của cung $\alpha$ thuộc góc phần tư thứ IV nên $\sin \alpha < 0, \cos \alpha > 0, \tan \alpha < 0.$

b) $3\pi < \alpha < \frac{10\pi}{3}.$

Ta có: điểm cuối của cung $\alpha$ thuộc góc phần tư thứ III nên $\sin \alpha < 0, \cos \alpha < 0, \tan \alpha > 0.$

c) $\frac{5\pi}{2} < \alpha < \frac{11\pi}{4}.$

Ta có: điểm cuối của cung $\alpha$ thuộc góc phần tư thứ II nên $\sin \alpha > 0, \cos \alpha < 0, \tan \alpha < 0.$

Ví dụ 8. Cho $0^\circ < \alpha < 90^\circ.$ Xét dấu các biểu thức sau:

a) $A = \cos (\alpha + 90^\circ).$

b) $B = \sin (\alpha + 80^\circ).$

Giải

a) $A = \cos (\alpha + 90^\circ) = \cos (90^\circ – (-\alpha)) = \sin (-\alpha) = -\sin \alpha.$

Vì $0^\circ < \alpha < 90^\circ$ nên $\sin \alpha > 0.$

Do đó $A < 0.$

b) $B = \sin (\alpha + 80^\circ).$

Vì $0^\circ < \alpha < 90^\circ$ nên $80^\circ < \alpha + 80^\circ < 170^\circ.$

Do đó, điểm cuối của cung $\alpha + 80^\circ$ thuộc góc phần tư thứ I hoặc thứ II nên $B > 0.$

Ví dụ 9. Cho $90^\circ < \alpha < 180^\circ.$ Xét dấu các biểu thức sau:

a) $A = \sin (270^\circ – \alpha).$

b) $B = \cos (2\alpha + 90^\circ).$

Giải

a) $A = \sin (270^\circ – \alpha).$

Vì $-180^\circ < -\alpha < -90^\circ$ nên $90^\circ < 270^\circ – \alpha < 180^\circ.$

Do đó, điểm cuối của cung $270^\circ – \alpha$ thuộc góc phần tư thứ II nên $A > 0.$

b) $B = \cos (2\alpha + 90^\circ).$

Ta có $B = \cos (2\alpha + 90^\circ) = \cos (90^\circ – (-2\alpha)) = \sin (-2\alpha) = -\sin (2\alpha).$

Vì $180^\circ < 2\alpha < 360^\circ$ nên $\sin (2\alpha) < 0.$

Do đó, $B > 0.$

Ví dụ 10. Cho $0 < \alpha < \frac{\pi}{2}.$ Xét dấu các biểu thức sau:

a) $A = \cos \left( \alpha + \frac{3\pi}{5} \right).$

b) $B = \cos \left( \alpha – \frac{\pi}{8} \right).$

Giải

a) $A = \cos \left( \alpha + \frac{3\pi}{5} \right).$

Vì $0 < \alpha < \frac{\pi}{2}$ nên $\frac{3\pi}{5} < \alpha + \frac{3\pi}{5} < \frac{11\pi}{10}.$

Do đó, điểm cuối của cung $\alpha + \frac{3\pi}{5}$ thuộc góc phần tư thứ II hoặc thứ III.

Vậy $A < 0.$

b) $B = \cos \left( \alpha – \frac{\pi}{8} \right).$

Vì $0 < \alpha < \frac{\pi}{2}$ nên $-\frac{\pi}{8} < \alpha – \frac{\pi}{8} < \frac{3\pi}{8}.$

Do đó, điểm cuối của cung $\alpha – \frac{\pi}{8}$ thuộc góc phần tư thứ IV hoặc thứ I.

Vậy $B > 0.$

Ví dụ 11. Cho $\pi < \alpha < \frac{3\pi}{2}.$ Xét dấu các biểu thức sau:

a) $A = \sin \left( \alpha + \frac{\pi}{2} \right).$

b) $B = \sin \left( \alpha + \frac{1119\pi}{2} \right).$

Giải

a) $A = \sin \left( {\alpha + \frac{\pi }{2}} \right)$ $ = \sin \left( {\frac{\pi }{2} – ( – \alpha )} \right)$ $ = \cos ( – \alpha )$ $ = \cos \alpha < 0.$

b) $B = \sin \left( {\alpha + \frac{{1119\pi }}{2}} \right)$ $ = \sin \left( {\alpha – \frac{\pi }{2} + 280 \cdot 2\pi } \right)$ $ = \sin \left( {\alpha – \frac{\pi }{2}} \right)$ $ = – \sin \left( {\frac{\pi }{2} – \alpha } \right)$ $ = – \cos \alpha > 0.$

Ví dụ 12. Cho tam giác $ABC.$ Xét dấu của biểu thức $P = \cos A \cdot \cos B \cdot \cos C$ trong các trường hợp:

a) Tam giác $ABC$ là tam giác nhọn.

b) Tam giác $ABC$ là tam giác tù.

Giải

a) Tam giác $ABC$ là tam giác nhọn.

Vì tam giác $ABC$ nhọn nên $A < 90^\circ, B < 90^\circ, C < 90^\circ$ hay $\cos A > 0, \cos B > 0, \cos C > 0.$

Vậy $P = \cos A \cdot \cos B \cdot \cos C > 0.$

b) Tam giác $ABC$ là tam giác tù.

Vì tam giác $ABC$ là tam giác tù nên $\triangle ABC$ có duy nhất một góc tù. Giả sử góc tù là góc $A \Rightarrow \cos A < 0$ và $\cos B > 0, \cos C > 0.$

Vậy $P = \cos A \cdot \cos B \cdot \cos C < 0.$

6. Lỗi thường gặp và mẹo ghi nhớ nhanh

• Nhầm dấu khi góc vượt $\pi$: luôn xác định lại góc phần tư sau khi rút gọn.
• Quên dấu trừ khi góc âm: nhớ công thức $\sin(-\alpha) = -\sin\alpha$, $\tan(-\alpha) = -\tan\alpha$.
• Cách nhớ nhanh bằng cụm từ:
  

  “Sin – Trên Trời, Cos – Dưới Đất, Tan – Trái Phải”

  (tượng trưng cho dấu dương của từng hàm theo góc phần tư).

Để nhớ được lâu, bạn hãy tải file pdf này về để rèn luyện:Tải file

7. Câu hỏi thường gặp

8. Tổng kết

Muốn biết dấu của $\sin\alpha$, $\cos\alpha$, $\tan\alpha$ → xác định góc phần tư của điểm cuối trên đường tròn lượng giác.

Khi gặp góc âm hoặc góc lớn, rút gọn về khoảng $[0,2\pi)$ trước.

Ghi nhớ quy tắc: “Sin dương góc I, II — Cos dương góc I, IV — Tan dương góc I, III.”