Trong hành trình học Toán, “góc” và “cung lượng giác” là hai khái niệm đầu tiên giúp học sinh bước vào thế giới lượng giác – nơi hình học và đại số hòa quyện thông qua vòng tròn.
Nếu như góc mô tả mức độ quay của một tia quanh điểm gốc, thì cung lượng giác lại thể hiện chiều dài quỹ đạo tương ứng trên đường tròn.
Việc hiểu rõ hai khái niệm này là bước đệm quan trọng để tiếp cận các nội dung nâng cao hơn như đường tròn lượng giác, giá trị sin – cos – tan của góc, hay các hàm số lượng giác trong chương trình THPT.
Bài viết này sẽ giúp bạn nắm vững:
- Khái niệm góc lượng giác và cung lượng giác,
- Cách đo góc bằng độ và radian,
- Công thức tính độ dài cung,
- Mối liên hệ giữa góc và cung,
- Ứng dụng thực tế trong Toán học và đời sống.
1. Góc lượng giác là gì?
1.1. Khái niệm góc trong hình học
Trong hình học cơ bản, góc được tạo bởi hai tia chung gốc.
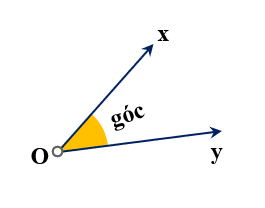
- Gốc chung gọi là đỉnh góc,
- Hai tia gọi là cạnh góc.
Đơn vị đo quen thuộc là độ (°), với:
- $1^\circ = 60’$ (phút),
- $1′ = 60”$ (giây).
Một vòng tròn đầy đủ tương ứng với $360^\circ$.
1.2. Góc lượng giác và chiều quay
Trong lượng giác, góc lượng giác không chỉ có độ mở mà còn có chiều quay.

Một góc lượng giác được xác định bởi:
- Tia gốc (thường là $\overrightarrow{Ox}$),
- Tia quay (thường là $\overrightarrow{OM}$),
- Chiều quay (ngược hoặc cùng chiều kim đồng hồ).
Quy ước:
- Quay ngược chiều kim đồng hồ → góc dương,
- Quay cùng chiều kim đồng hồ → góc âm.
Ký hiệu thường dùng: $(\overrightarrow{Ox}, \overrightarrow{OM}) = \alpha$
Điều này cho phép chúng ta mô tả nhiều góc khác nhau có cùng vị trí trên đường tròn, ví dụ $\alpha$, $\alpha + 2\pi$, $\alpha – 2\pi$, v.v.
2. Đơn vị đo góc: Độ và Radian
2.1. Góc đo bằng độ
Độ (°) là đơn vị phổ biến trong hình học cơ bản.
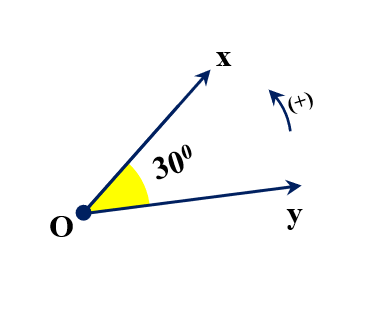
Một vòng tròn được chia thành 360 phần bằng nhau: $1 \text{ vòng} = 360^\circ$
Tuy nhiên, trong lượng giác, đơn vị này không thuận tiện cho tính toán công thức, vì thế người ta sử dụng radian.
2.2. Góc đo bằng radian
Radian là đơn vị tự nhiên của góc trong toán học.
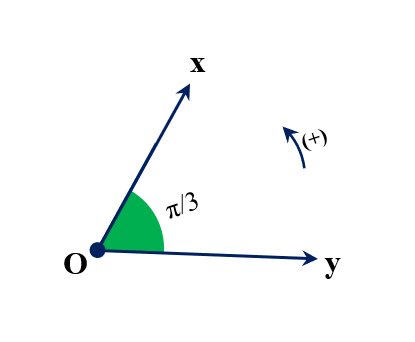
Định nghĩa: Một góc có số đo 1 radian nếu nó chắn một cung có độ dài bằng bán kính của đường tròn.
Công thức chung: $\alpha = \frac{l}{R}$
Trong đó:
- $\alpha$: số đo góc ở tâm (tính bằng radian),
- $l$: độ dài cung chắn bởi góc đó,
- $R$: bán kính của đường tròn.
Do chu vi của đường tròn bằng $2\pi R$ nên: $2\pi \text{ rad} = 360^\circ$
2.3. Công thức đổi giữa độ và radian
Từ mối quan hệ trên, ta có: $180^\circ = \pi \text{ rad}$
Suy ra công thức đổi:
- Từ độ sang radian: $\alpha_{\text{rad}} = \alpha_{\text{độ}} \times \frac{\pi}{180}$
- Từ radian sang độ: $\alpha_{\text{độ}} = \alpha_{\text{rad}} \times \frac{180}{\pi}$
Ví dụ:
$60^\circ = 60 \times \frac{\pi}{180} = \frac{\pi}{3} \text{ rad}$
$\frac{\pi}{2} \text{ rad} = \frac{\pi}{2} \times \frac{180}{\pi} = 90^\circ$
3. Cung lượng giác là gì?
3.1. Định nghĩa cung lượng giác
Trên đường tròn tâm $O$, cung lượng giác là phần của đường tròn bị giới hạn bởi hai bán kính.
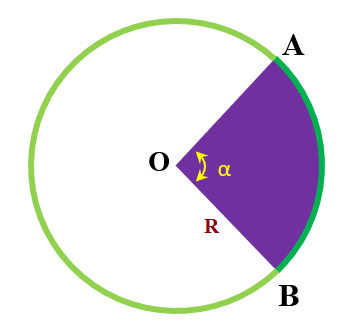
Nếu góc ở tâm là $\alpha$ (đo bằng radian), ta có thể xác định độ dài cung tương ứng bằng công thức sau.
3.2. Công thức tính độ dài cung lượng giác
$l = R\alpha$
Trong đó:
- $l$: độ dài cung,
- $R$: bán kính đường tròn,
- $\alpha$: góc ở tâm (đo bằng radian).
Công thức này cho thấy độ dài cung tỉ lệ thuận với góc ở tâm – nếu góc gấp đôi, cung cũng dài gấp đôi.
3.3. Trường hợp đặc biệt
| Góc ở tâm $\alpha$ | Độ dài cung $l$ | Ghi chú |
|---|---|---|
| $\alpha = \pi$ | $l = \pi R$ | Nửa đường tròn |
| $\alpha = 2\pi$ | $l = 2\pi R$ | Toàn bộ đường tròn |
Ví dụ:
Nếu $R = 5 \text{ cm}$ và $\alpha = \frac{\pi}{3}$
thì $l = 5 \times \frac{\pi}{3} = \frac{5\pi}{3} \text{ cm}$.
4. Mối liên hệ giữa góc và cung lượng giác
4.1. Công thức liên hệ
Giữa góc lượng giác và cung lượng giác luôn có mối quan hệ: $ l = R\alpha $
Đây là công thức cơ bản, giúp chuyển đổi giữa độ dài (đơn vị mét, cm) và góc quay (đơn vị radian).
Khi $R = 1$ (trên đường tròn lượng giác), ta có: $ l = \alpha $
→ Độ dài cung chính bằng số đo của góc.
4.2. Góc dương, góc âm và chiều cung
- Nếu $\alpha > 0$ → cung quay ngược chiều kim đồng hồ (cung dương).
- Nếu $\alpha < 0$ → cung quay theo chiều kim đồng hồ (cung âm).
Như vậy, trên đường tròn lượng giác, chiều quay quyết định dấu của góc và chiều của cung.
4.3. Các góc có cùng vị trí (góc đồng vị trí)
Khi ta quay nhiều vòng quanh đường tròn, vị trí điểm cuối không thay đổi dù góc đã vượt quá $2\pi$.
Vì thế, ta có: $\alpha’ = \alpha + 2k\pi \quad (k \in \mathbb{Z})$
Các góc như vậy được gọi là góc cùng phương (đồng vị trí).
Chúng sẽ có cùng giá trị lượng giác (ví dụ: cùng sin, cos, tan).
5. Ứng dụng của góc và cung lượng giác
5.1. Trong chương trình THCS
- Giúp học sinh xác định và đo góc trong hình học phẳng.
- Tính độ dài cung tròn, chu vi hình tròn, diện tích hình quạt.
- Rèn luyện khả năng liên hệ giữa hình học và đại lượng thực tế.
Ví dụ: Tính độ dài cung tròn của bánh xe có bán kính 20 cm quay một góc $60^\circ$: $\alpha = \frac{\pi }{3}$ $ \Rightarrow l = 20 \times \frac{\pi }{3} = \frac{{20\pi }}{3}{\rm{ cm}}$
5.2. Trong chương trình THPT
- Là nền tảng của đường tròn lượng giác (bán kính $R = 1$).
- Liên quan trực tiếp đến định nghĩa các giá trị lượng giác: $\sin\alpha, \cos\alpha, \tan\alpha$
- Giúp hiểu rõ tính chu kỳ của các hàm lượng giác.
- Ứng dụng trong dao động điều hòa, chuyển động tròn đều.
5.3. Trong đời sống thực tế
Các khái niệm về góc và cung lượng giác xuất hiện khắp nơi:
- Kim đồng hồ quay một góc $30^\circ$ sau mỗi 5 phút,
- Bánh xe, bánh răng, cánh quạt đều hoạt động dựa trên góc quay,
- Quỹ đạo hành tinh mô phỏng chuyển động tròn trong không gian.
Nhờ đó, học sinh có thể thấy lượng giác không chỉ là lý thuyết, mà còn hiện diện trong mọi chuyển động quanh ta.
6. Tóm tắt kiến thức quan trọng
6.1. Bảng tổng hợp công thức
| Nội dung | Công thức | Ghi chú |
|---|---|---|
| Định nghĩa radian | $\alpha = \frac{l}{R}$ | Số đo góc ở tâm |
| Mối quan hệ độ – radian | $180^\circ = \pi \text{ rad}$ | Dùng để đổi đơn vị |
| Độ dài cung lượng giác | $l = R\alpha$ | Khi $\alpha$ tính bằng radian |
| Góc đồng vị trí | $\alpha’ = \alpha + 2k\pi$ | $k \in \mathbb{Z}$ |
6.2. Bảng quy đổi nhanh giữa độ và radian
| Độ (°) | Radian (rad) |
|---|---|
| 30° | $\pi/6$ |
| 45° | $\pi/4$ |
| 60° | $\pi/3$ |
| 90° | $\pi/2$ |
| 180° | $\pi$ |
| 360° | $2\pi$ |
7. FAQs
1️⃣ Hỏi: Cách đo góc bằng radian như thế nào?
Trong lượng giác, radian được định nghĩa dựa trên độ dài cung của đường tròn.
Nếu đường tròn có bán kính là $R$ và cung tròn có độ dài $l$, thì số đo góc ở tâm tính bằng radian là: $\alpha = \frac{l}{R}$
Khi cung tròn có độ dài bằng đúng bán kính ($l = R$), thì góc ở tâm đó có số đo 1 radian. Một vòng tròn đầy đủ tương ứng với $2\pi$ radian hay $360^\circ$
2️⃣ Hỏi: Sự khác nhau giữa độ và radian trong lượng giác là gì?
Cả độ (degree) và radian đều dùng để đo góc, nhưng đơn vị và ứng dụng khác nhau:
Trong độ: Một vòng tròn đầy đủ là $360^\circ$.
Trong radian: Một vòng tròn đầy đủ là $2\pi$.
Hai đơn vị này quy đổi cho nhau bằng công thức: $1~\text{radian} = \frac{180}{\pi}^\circ, \quad 1^\circ = \frac{\pi}{180}~\text{radian}$
Trong toán học nâng cao, radian thường được dùng vì giúp các công thức lượng giác trở nên ngắn gọn và dễ xử lý hơn.
3️⃣ Hỏi: Công thức tính độ dài cung theo radian là gì?
Độ dài cung tròn là khoảng cách dọc theo đường cong giữa hai điểm trên đường tròn.
Nếu góc ở tâm có số đo $\alpha$ (radian) và bán kính đường tròn là $R$, thì độ dài cung $l$ được tính theo công thức: $l = R \times \alpha$
Nếu góc được cho bằng độ, cần đổi sang radian trước khi tính: $l = R \times \frac{\pi \times \alpha}{180}$
4️⃣ Hỏi: Mối quan hệ giữa góc ở tâm và cung tròn là gì?
Trong cùng một đường tròn, góc ở tâm và độ dài cung tròn mà nó chắn được có mối quan hệ tỉ lệ thuận: $\frac{l_1}{l_2} = \frac{\alpha_1}{\alpha_2}$
Nói cách khác, nếu tăng gấp đôi góc ở tâm thì độ dài cung cũng tăng gấp đôi.
Đây là nguyên lý cơ bản giúp định nghĩa đơn vị đo góc radian trong lượng giác.
5️⃣ Hỏi: Radian là gì trong đường tròn?
Radian là đơn vị đo góc được xác định dựa trên tỉ số giữa độ dài cung tròn và bán kính của đường tròn.
Một góc ở tâm có số đo 1 radian khi cung tròn của nó có độ dài bằng bán kính ($l = R$).
Vì chu vi đường tròn bằng $2\pi R$, nên một vòng tròn đầy đủ tương ứng với: $360^\circ = 2\pi~\text{radian}
$Radian giúp biểu diễn góc trong các công thức lượng giác, đạo hàm, sóng, dao động điều hòa một cách tự nhiên và chính xác hơn.
7. Kết luận
Góc và cung lượng giác là nền tảng quan trọng nhất khi học lượng giác.
Chúng giúp ta hiểu sự quay, chu kỳ, và tính tuần hoàn — những đặc điểm đặc trưng của các hàm lượng giác.
Khi đã nắm vững phần này, bạn đã sẵn sàng bước sang chủ đề tiếp theo: Đường tròn lượng giác và cách xác định giá trị sin, cos, tan của một góc.